Lanqiu Yao

Lanqiu Yao

Ph.D. student at NYU Grossman School of Medicine

Posts by Collection

portfolio

publications

Properties and pitfalls of weighting as an alternative to multilevel multiple imputation in cluster randomized trials with missing binary outcomes under covariate-dependent missingness

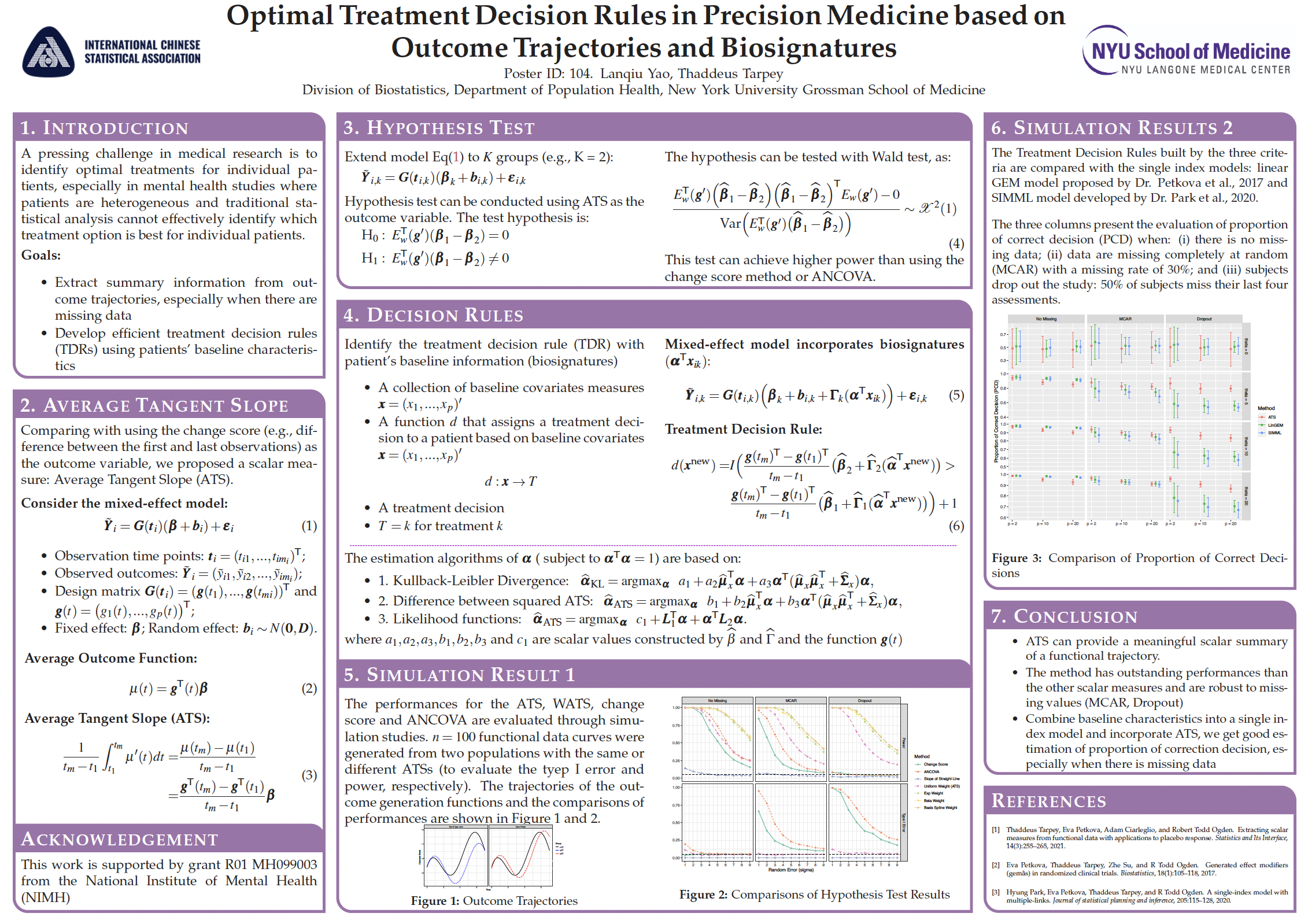
Published in Statistical Methods in Medical Research, 2009

This paper is about handling missing data in cluster randomize trials

Recommended citation: Turner, Elizabeth L., et al. "Properties and pitfalls of weighting as an alternative to multilevel multiple imputation in cluster randomized trials with missing binary outcomes under covariate-dependent missingness." Statistical methods in medical research 29.5 (2020): 1338-1353 https://github.com/sakuramomo1005/sakuramomo1005.github.io/blob/master/files/paper1.pdf

Engineering Escherichia coli to bind to cyanobacteria

Published in Journal of Bioscience and Bioengineering, 2017

This paper is about engineered Escherichia coli cells to bind to cyanobacteria by heterologously producing and displaying lectins of the target cyanobacteria on their surface

Recommended citation: Zhang, Zijian, et al. "Engineering Escherichia coli to bind to cyanobacteria." Journal of bioscience and bioengineering 123.3 (2017): 347-352. https://github.com/sakuramomo1005/sakuramomo1005.github.io/blob/master/files/paper2.pdf

talks

Discovering linear biosignatures for treatment response based on maximizing Kullback-Leibler Divergence in linear mixed-effect models

Published:

Abstract: It is a continuing challenge in mental health research to identify patients who respond to treatment, since the treated and untreated patients often have similar outcomes on average. Precision medicine approaches, that consider an individual’s personal information, often produce treatment decision rules that are quite complicated. In this talk, I provide an approach to precision medicine to estimate a linear combination of patient baseline characteristics, i.e., a “biosignature”, defined to maximize the Kullback-Leibler Divergence between a treatment and control distribution. I will describe an algorithm to estimate the biosignature and illustrate the approach via a simulation study and a depression clinical trial.

A Single Index Model for Longitudinal Outcomes to Optimize Individual Treatment Decision Rules

Published:

A pressing challenge in medical research is to identify optimal treatments for individual patients. This is particularly challenging in mental health settings where mean responses are often similar across multiple treatments. This talk investigates a potentially powerful precision medicine approach to this problem by examining the impact of baseline covariates on longitudinal outcome trajectories instead of scalar outcome measures. For example, on average, patients treated with an active drug versus placebo may have similar trajectories, but specific trajectory shapes may be unique to individuals treated with the active medication. We introduce a method of estimating “biosignatures” defined as linear combinations of baseline characteristics (i.e., a single index) that optimally separate longitudinal trajectories among different treatment groups. The criterion used is to maximize the Kullback-Leibler Divergences between different treatment outcome distributions. The approach is illustrated via simulation studies and a depression clinical trial. The comparison of the method with other approaches is also presented.

Extracting Scalar Measures from Functional Data withMissingness

Published:

It is increasingly common in practice to observe functional data(including longitudinal data) consisting of curves. It is oftennecessary to extract a scalar summary from functional data. Forexample, a scalar summary may be needed to compare treatments with nonlinear longitudinal outcomes. In precisionmedicine, scalar summaries of functional data are useful fordefining optimal treatment decision rules. In practice, scalarsummaries of functional data that are commonly used areinefficient because they ignore the functional information orlead to biased results (e.g., change scores or the slope of afitted line). These inefficiencies are usually compounded in thepresence of missing data. In this talk, we introduce a scalarmeasure from a functional observation based on a weightedaverage tangent slope (WATS). Since the tangent sloperepresents an instantaneous rate of improvement ordeterioration, an appropriately weighted average tangentslope can produce a useful summary from a functionalobservation that incorporates the shape of the trajectory. Inthis talk, we illustrate the WATS and demonstrate thatestimators of the WATS provide superior summaries offunctional data.

Extracting Scalar Measures from Functional Data withMissingness

Published:

It is increasingly common in practice to observe functional data(including longitudinal data) consisting of curves. It is oftennecessary to extract a scalar summary from functional data. Forexample, a scalar summary may be needed to compare treatments with nonlinear longitudinal outcomes. In precisionmedicine, scalar summaries of functional data are useful fordefining optimal treatment decision rules. In practice, scalarsummaries of functional data that are commonly used areinefficient because they ignore the functional information orlead to biased results (e.g., change scores or the slope of afitted line). These inefficiencies are usually compounded in thepresence of missing data. In this talk, we introduce a scalarmeasure from a functional observation based on a weightedaverage tangent slope (WATS). Since the tangent sloperepresents an instantaneous rate of improvement ordeterioration, an appropriately weighted average tangentslope can produce a useful summary from a functionalobservation that incorporates the shape of the trajectory. Inthis talk, we illustrate the WATS and demonstrate thatestimators of the WATS provide superior summaries offunctional data.

teaching